Simulation Numérique
Qu'est-ce que la Simulation Numérique par éléments-finis ?
Où comment utiliser la puissance de la modélisation par éléments-finis ?
De nombreux comportements physiques sont régis par des équations aux dérivées partielles (EDP). Ces équations étant insolvables analytiquement, la méthode de calcul par éléments finis permet de les résoudre numériquement : cela permet d’avoir une solution approchée d’un problème physique.
Simulation numérique : objectif de la démarche
- Identification du problème : phénomène à étudier, domaine d’utilisation
- Analyse des interactions avec l’extérieur (conditions aux limites)
- Analyse du comportement à étudier (état initial et évolutions)
Modélisation
La modélisation numérique est la transcription du phénomène physique en langage informatique.
Concrètement, le modèle numérique se construit en plusieurs étapes :
- Dessin de la structure à étudier et éventuelle décomposition du système en structures calculables (simplification du modèle, pièces non étudiées déterminées rigides et indéformables)
- Définition des propriétés du modèle :
- Caractéristiques matériaux
- Conditions aux limites et interactions
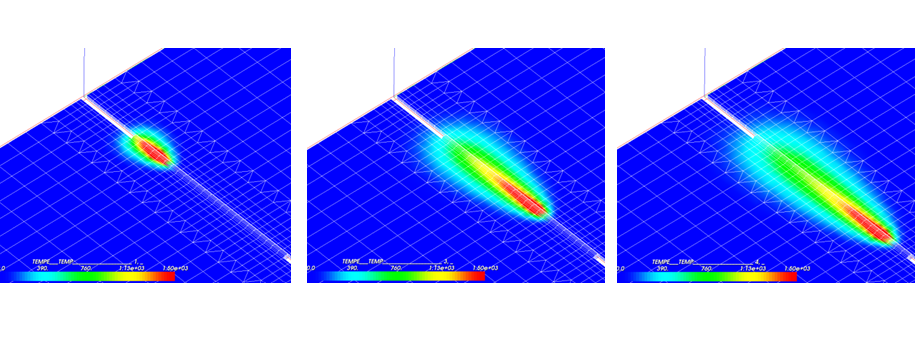
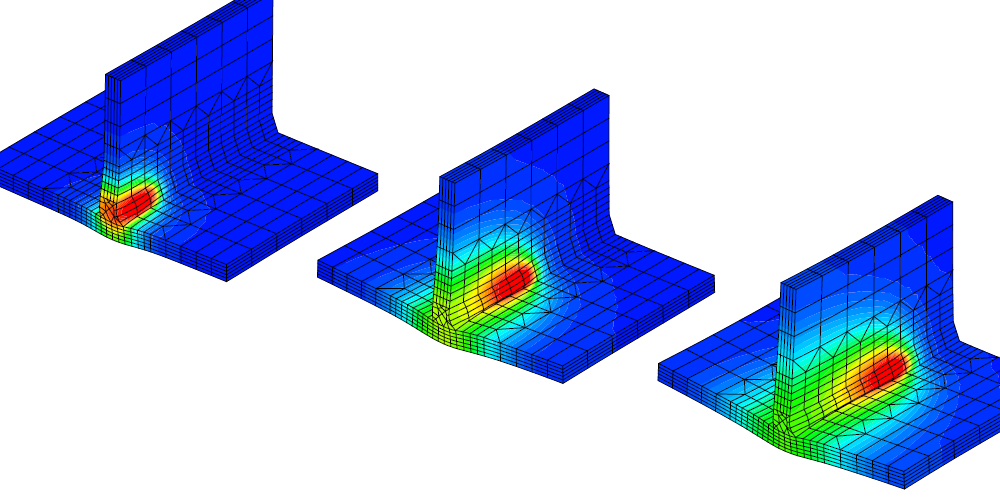
- Chargements qui peuvent être sous différentes formes : vitesse, déplacement, effort, température…
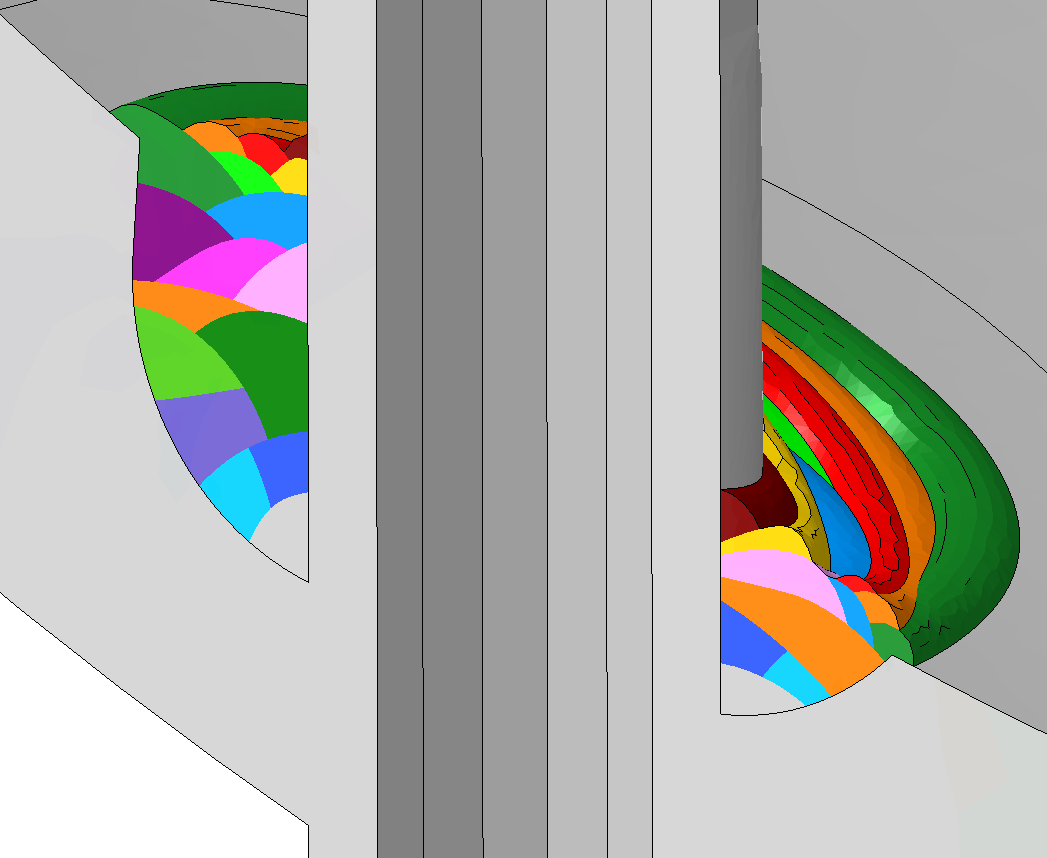
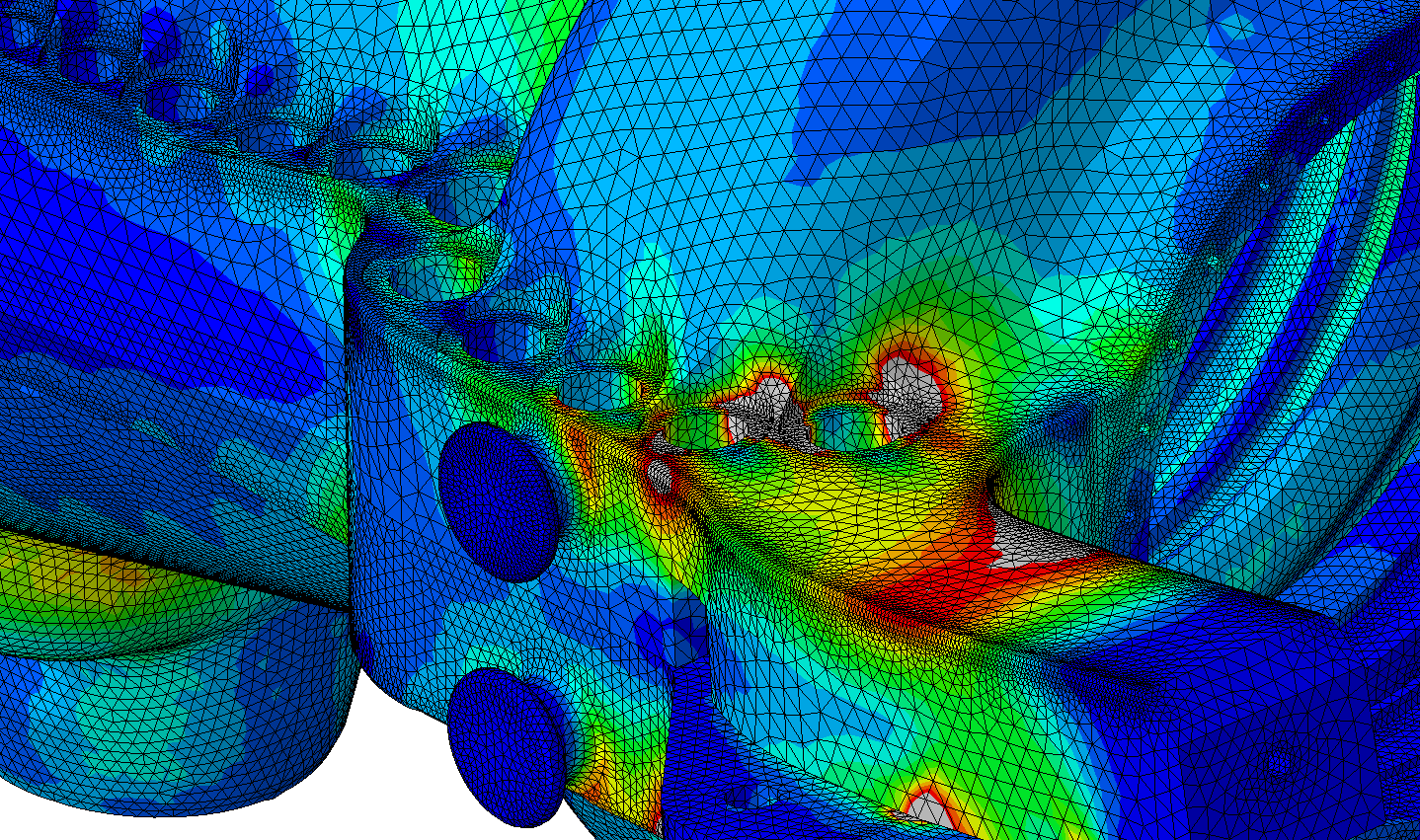
Discrétisation
Le modèle numérique de la structure étant composé d’une infinité de points, il est impossible de résoudre les équations aux dérivées partielles, même numériquement. La structure est donc découpée en un nombre fini de points qui se traduit par une décomposition de la géométrie en forme simple. L’ensemble de ces nœuds et éléments constituent le maillage du modèle.
Simulation numérique
Le solveur du code utilisé résout de manière approchée les équations en chaque nœud du maillage, en respectant les principes fondamentaux de la physique (conservation de masse et d’énergies).
En effet, en chaque nœud, l’une des deux composantes suivantes est connue : son déplacement ou la force extérieure appliquée. En supposant un comportement linéaire de la structure, la relation effort déplacement s’écrit {F} = [K].{q}. Les deux composantes peuvent ainsi être déterminées pour chacun des nœuds du modèle à chaque pas du calcul.
Post-traitement, analyse et interprétation des résultats
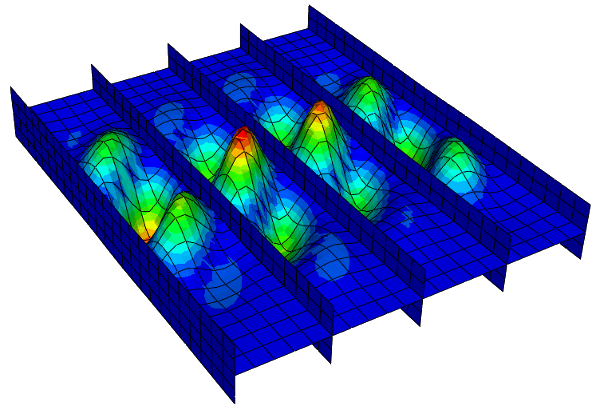
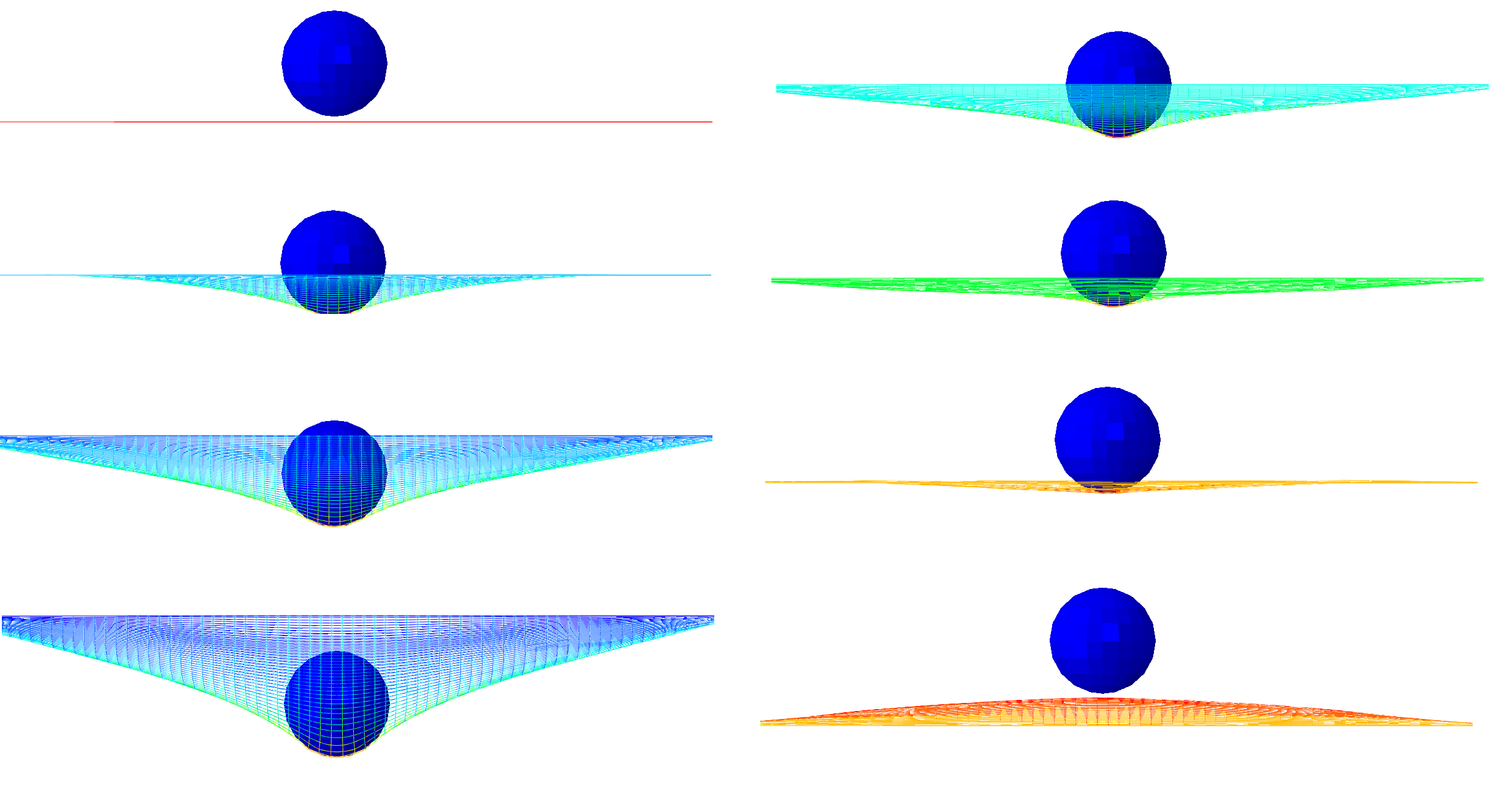
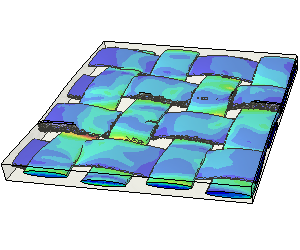
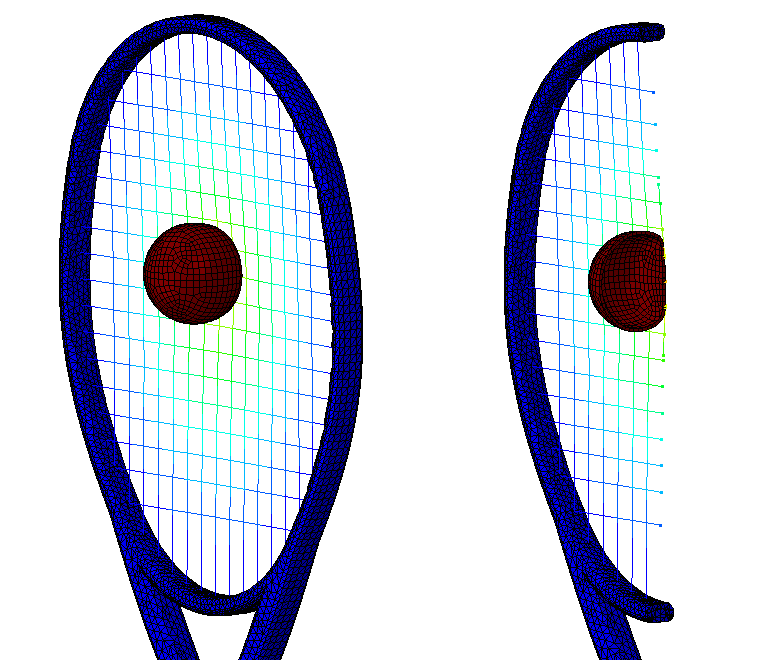
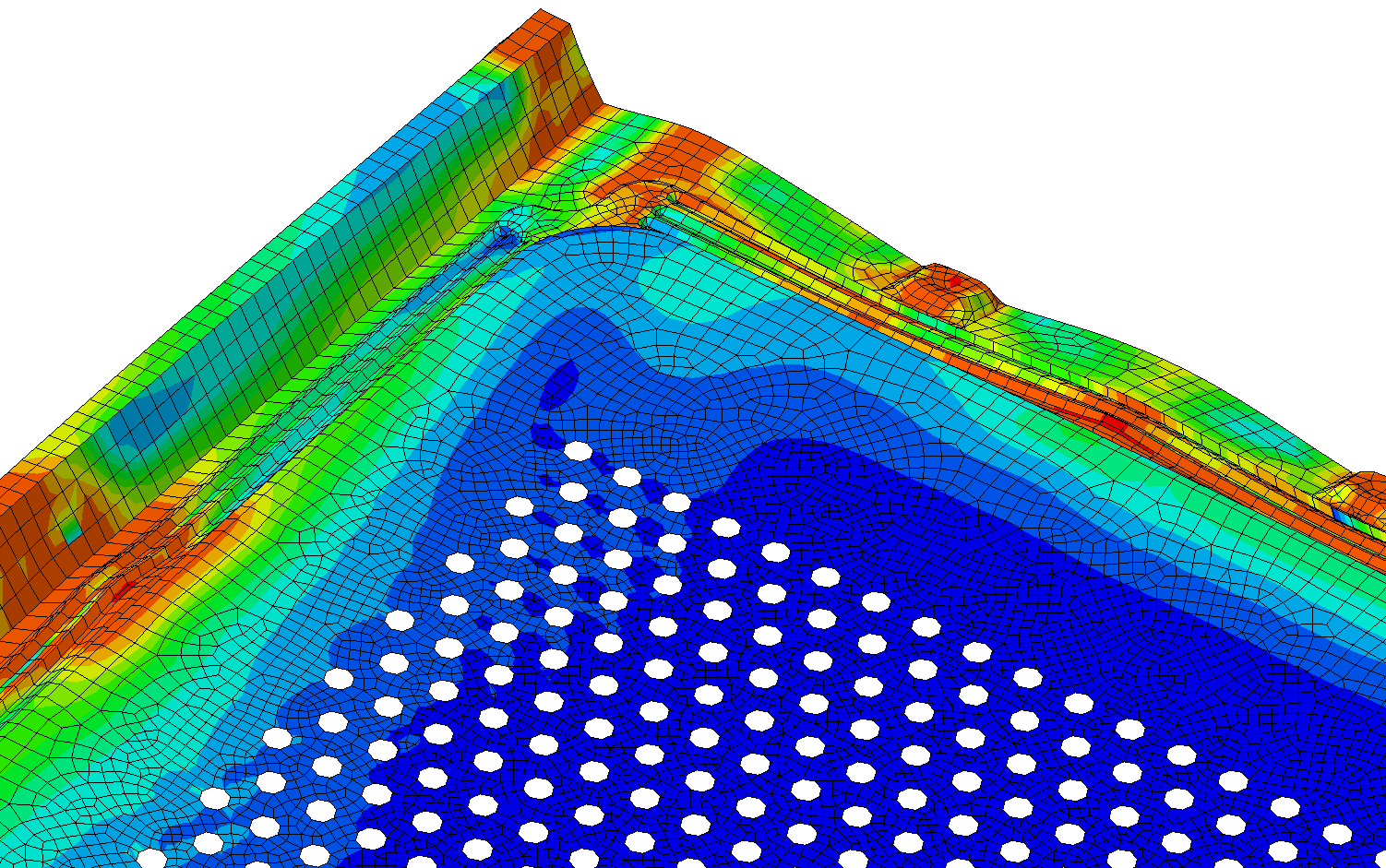
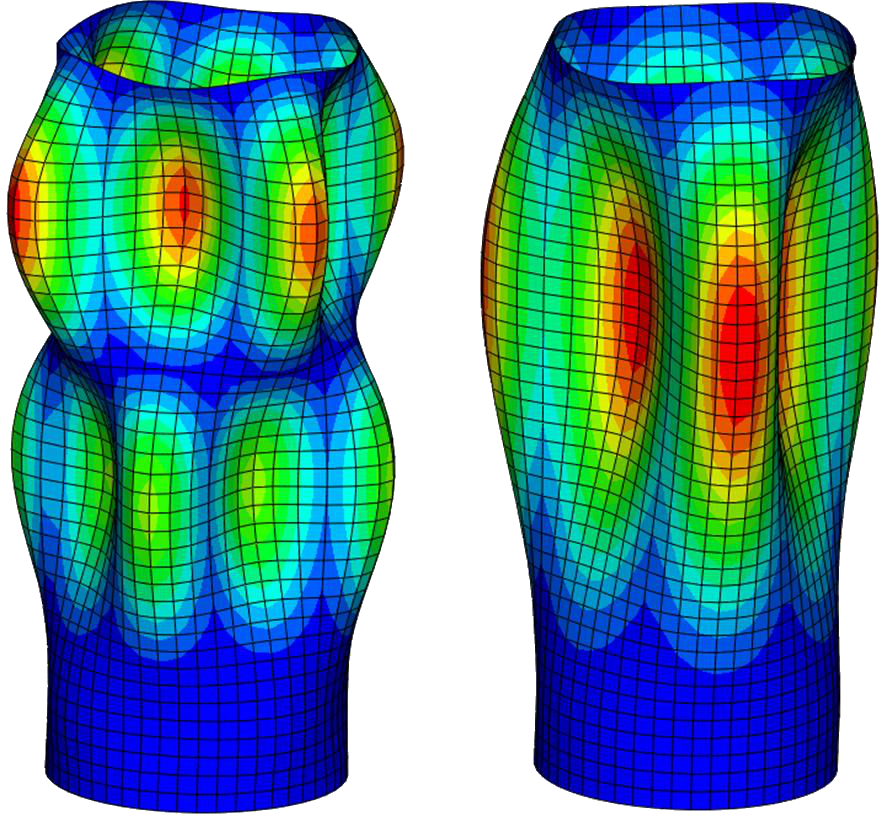
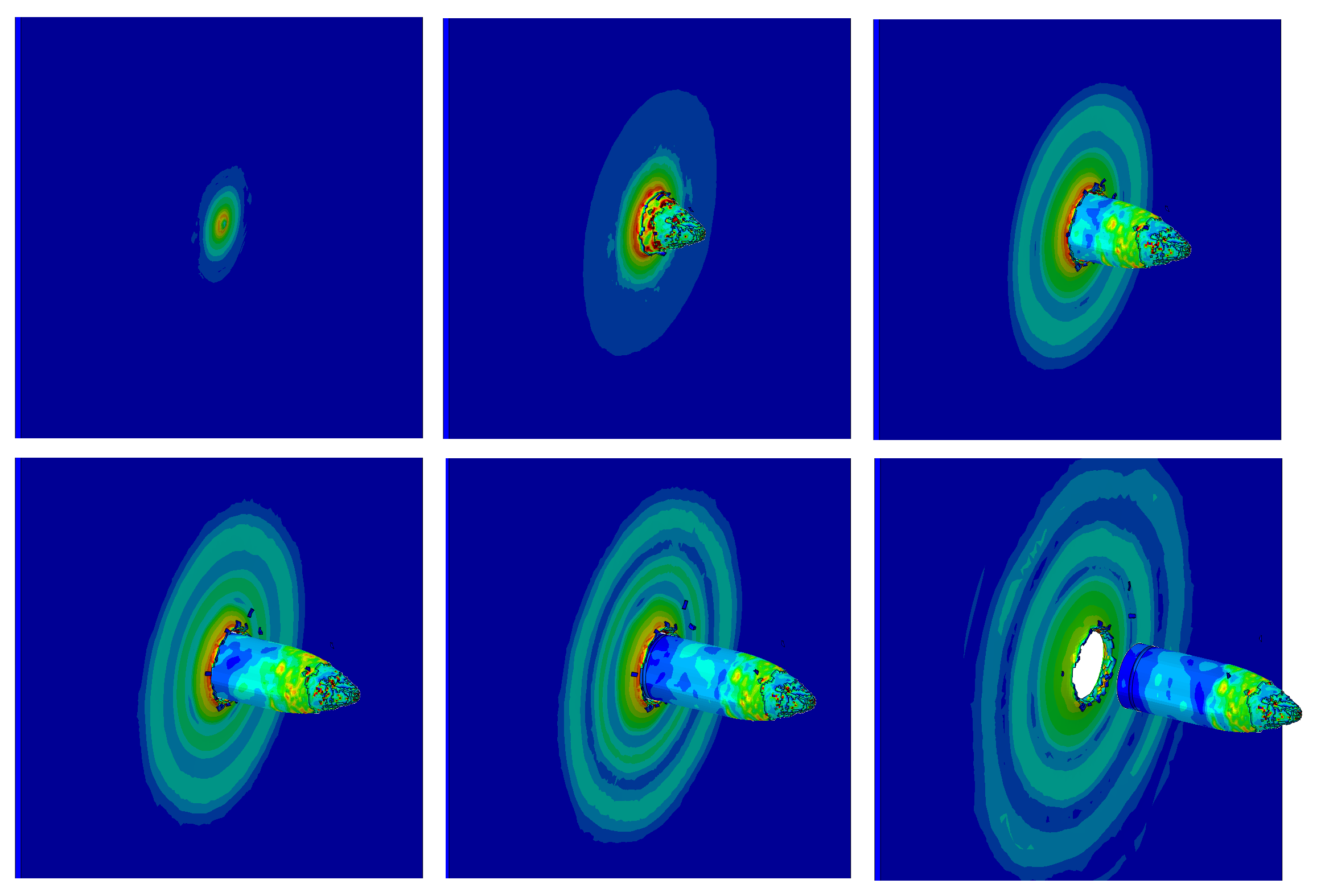
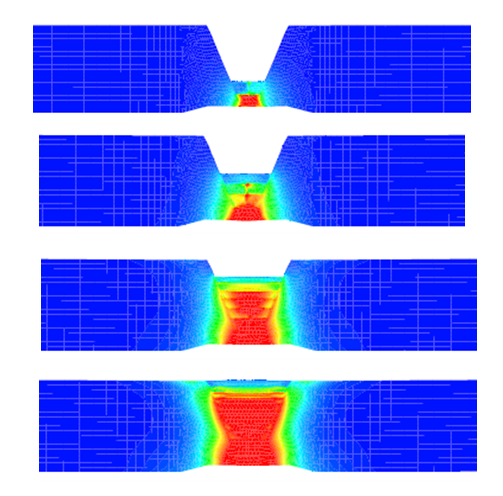
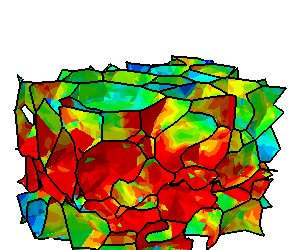
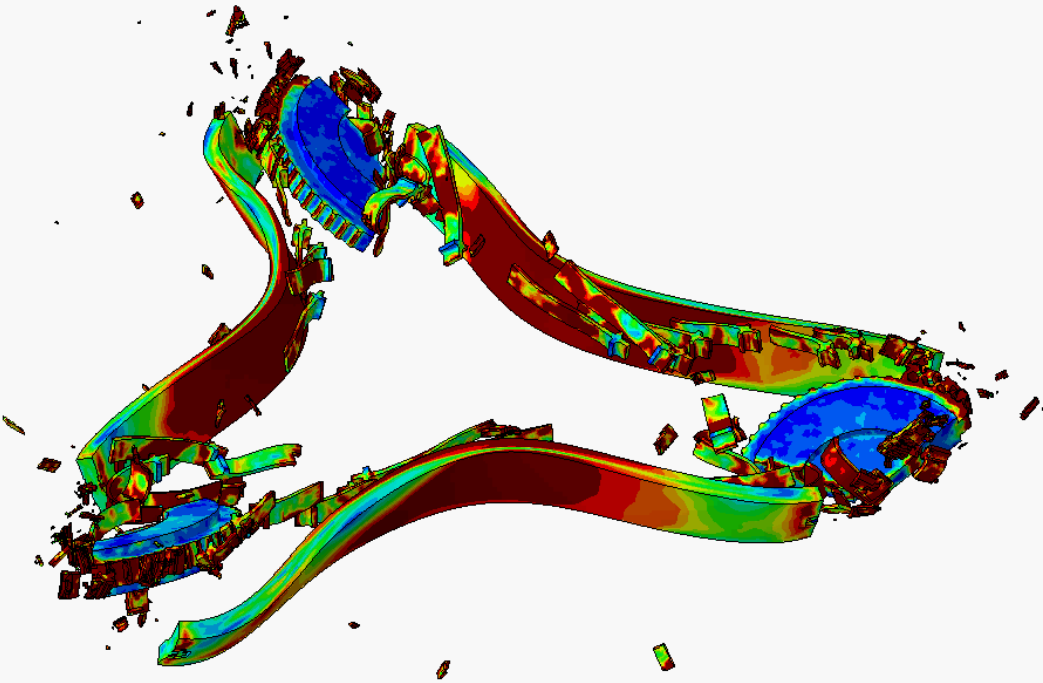
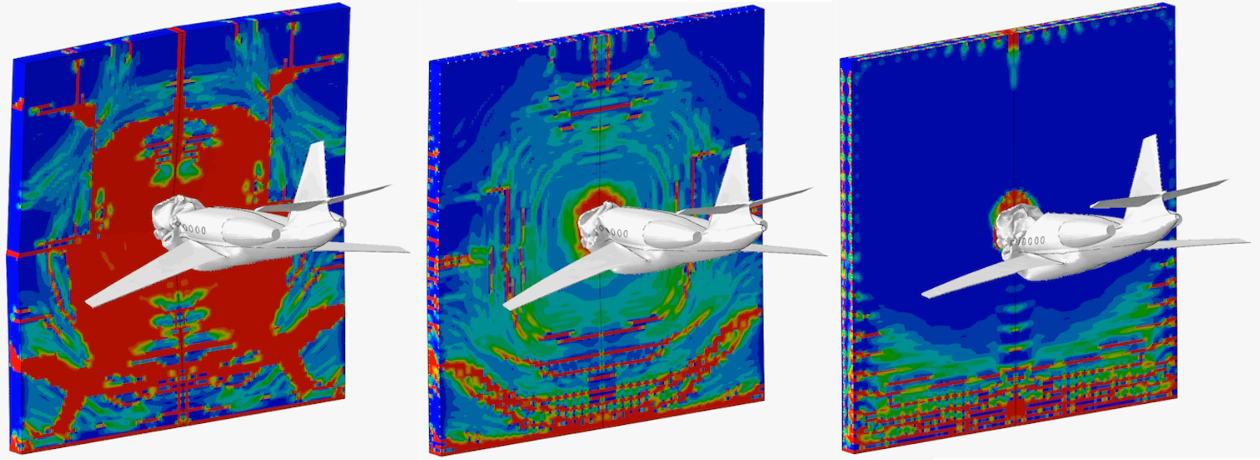
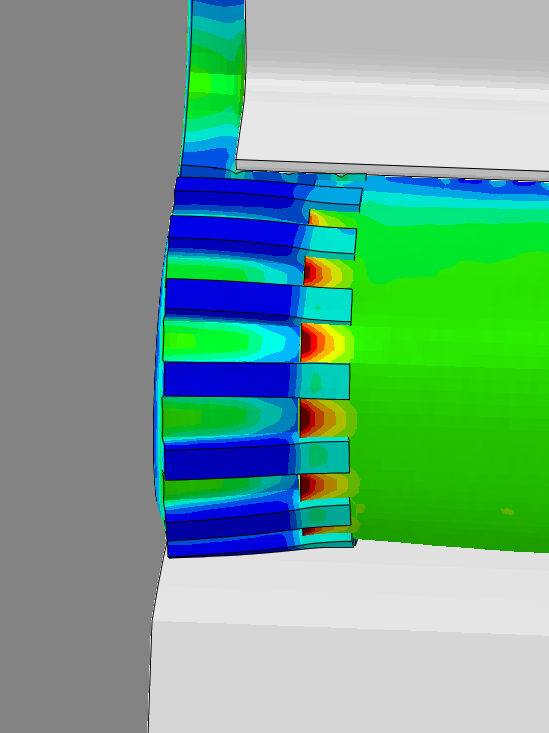
Les résultats sont visualisés à l’aide de l’interface graphique du logiciel de calcul. Le phénomène peut alors être observé à chaque incrément. Plusieurs paramètres peuvent être affichés en fonction du post-traitement voulu :
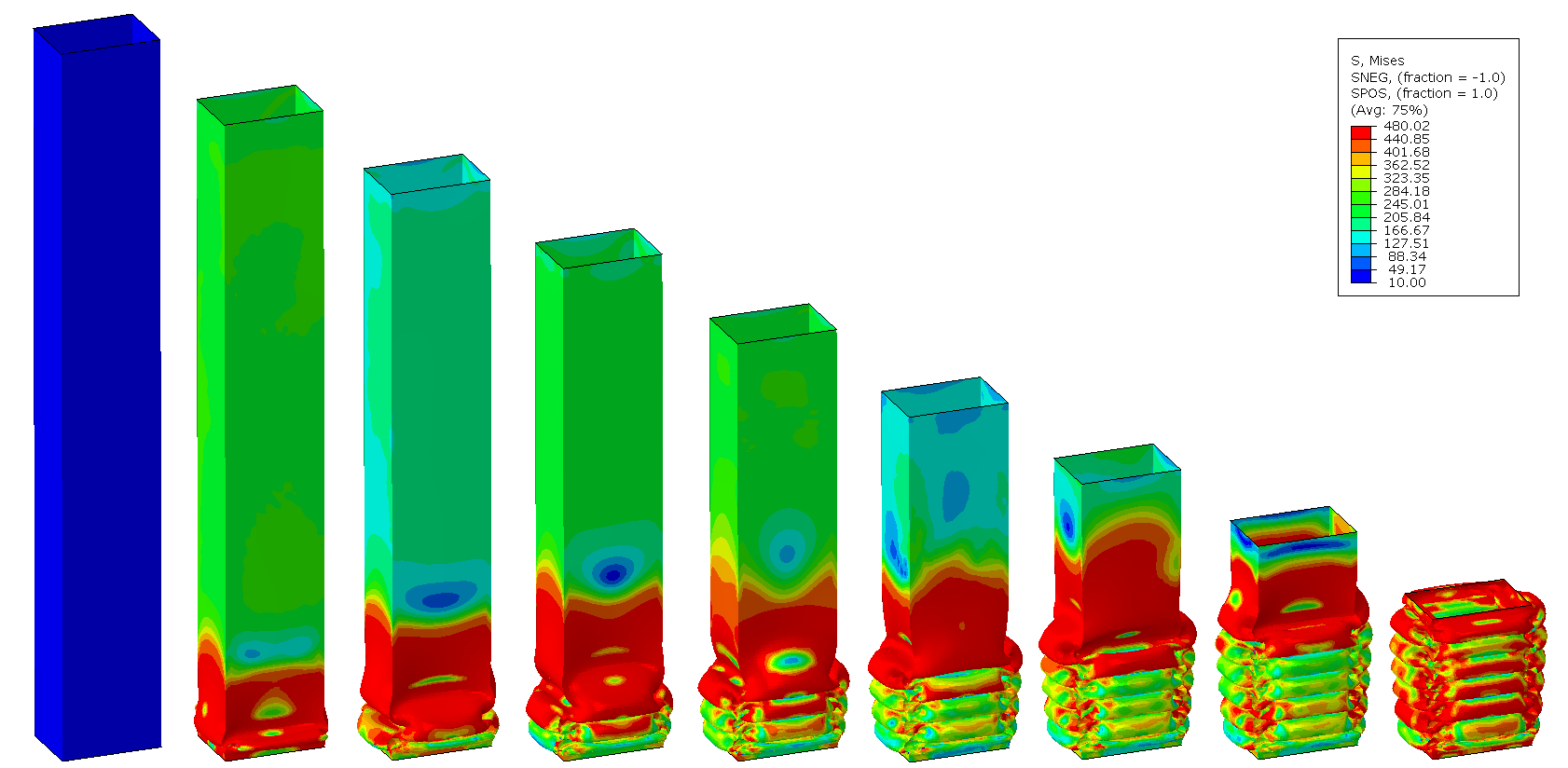
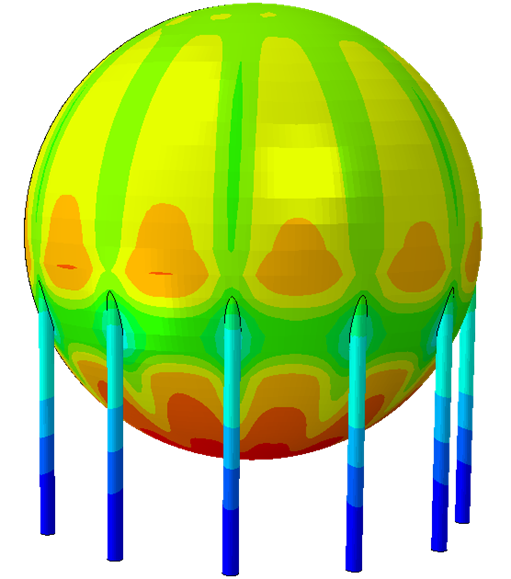
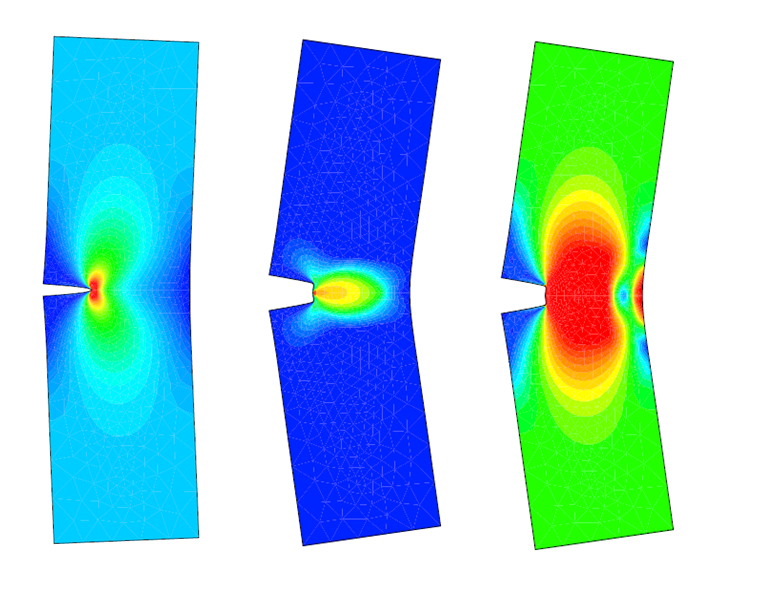
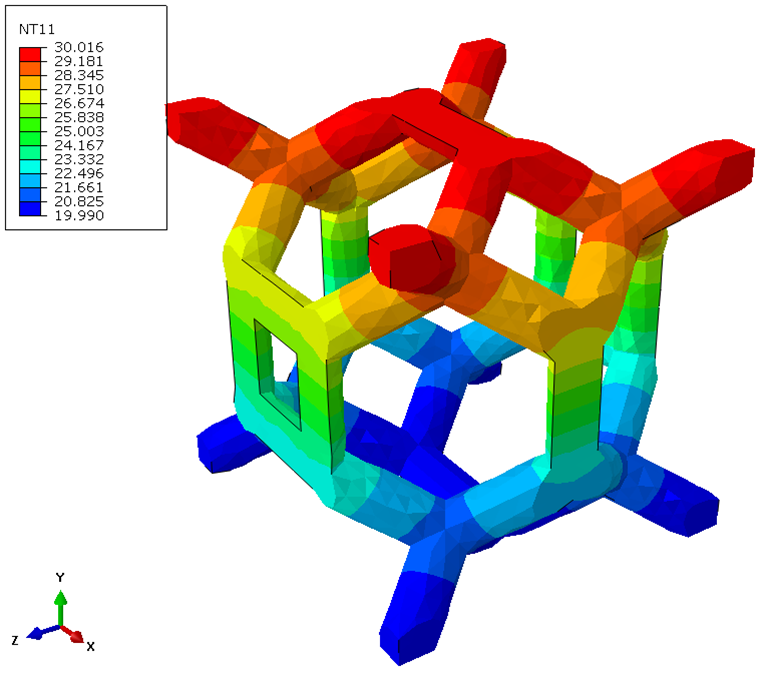
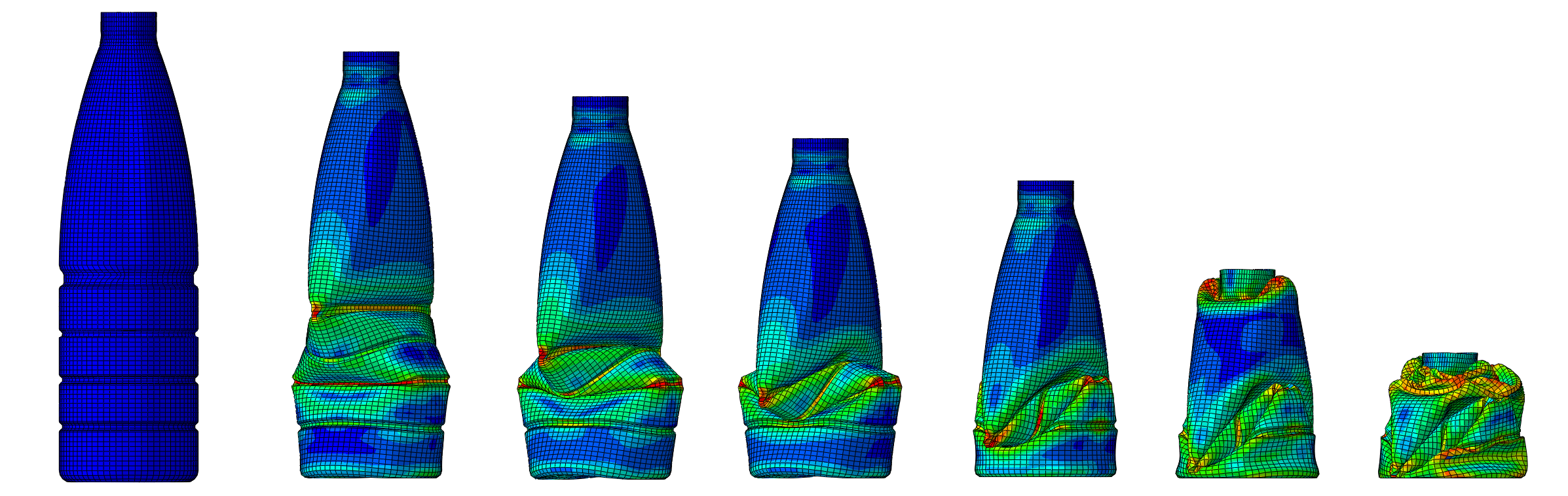
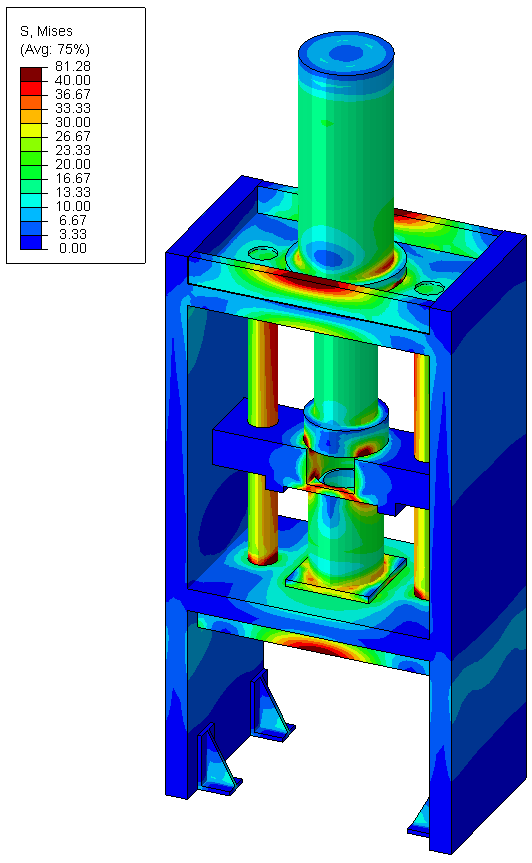
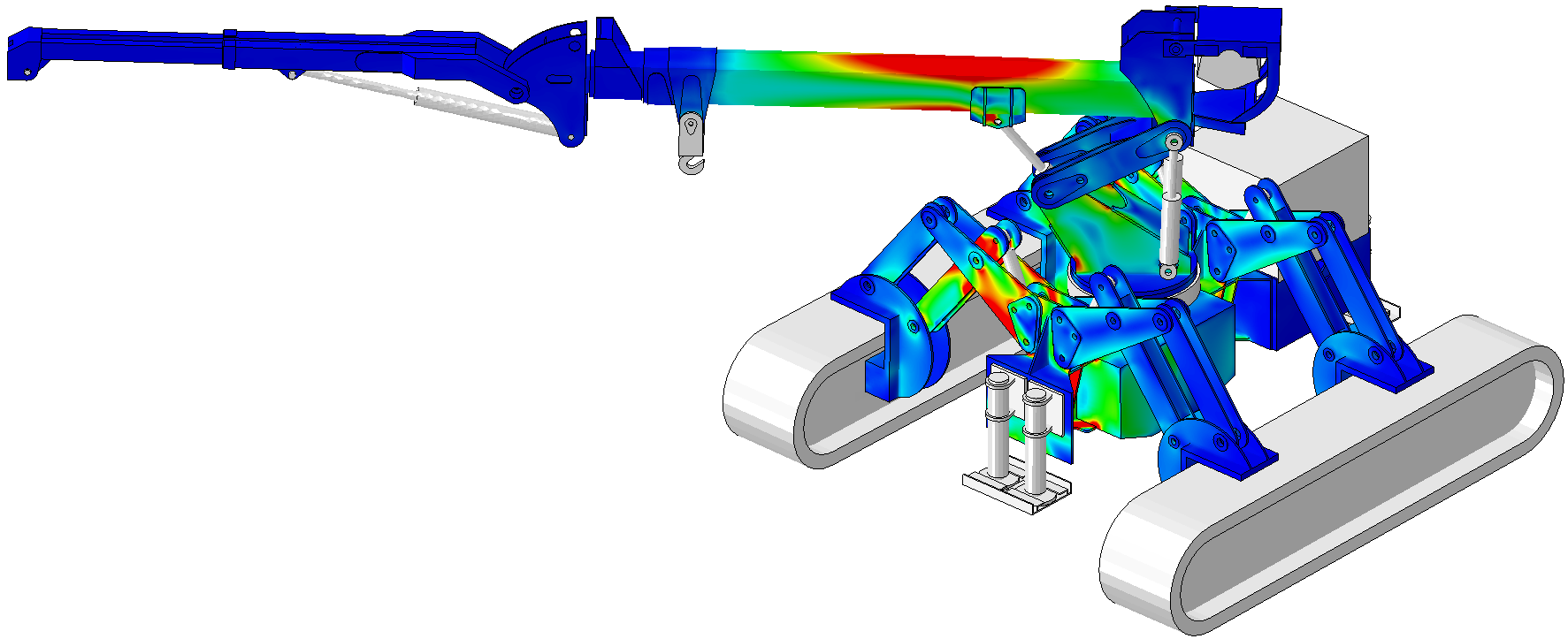
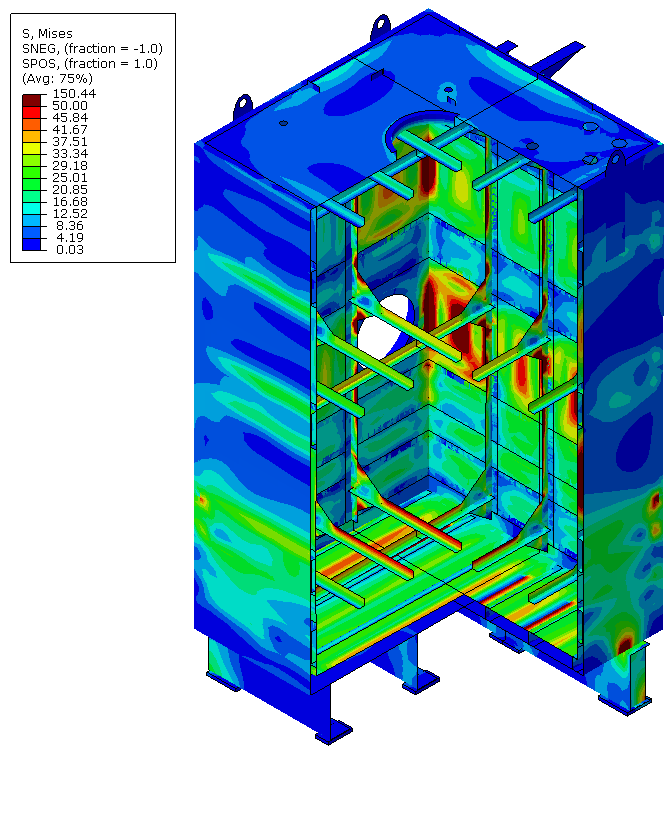
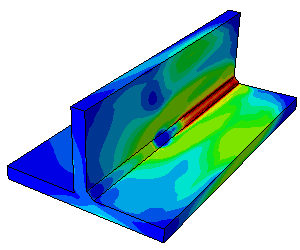
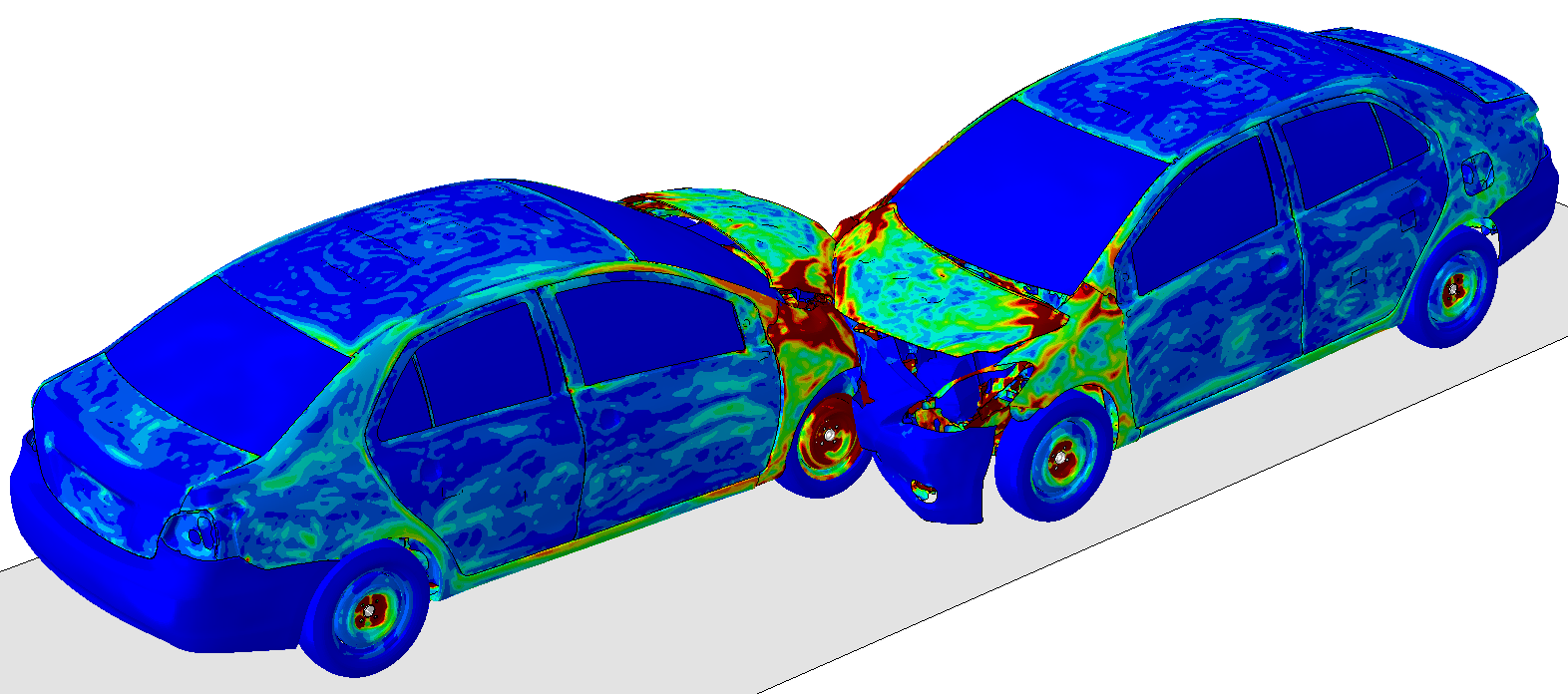
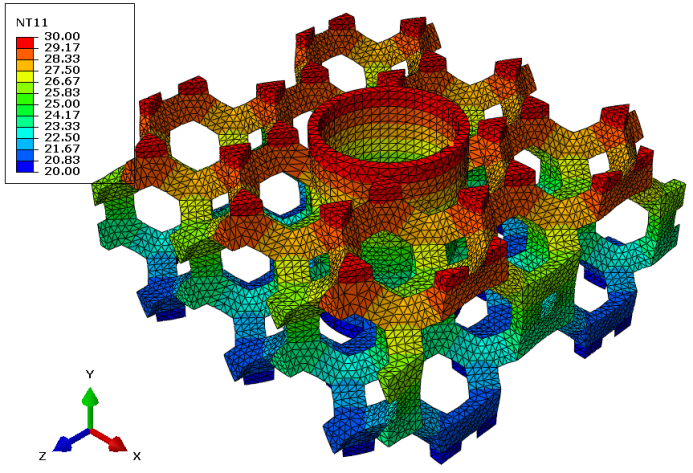
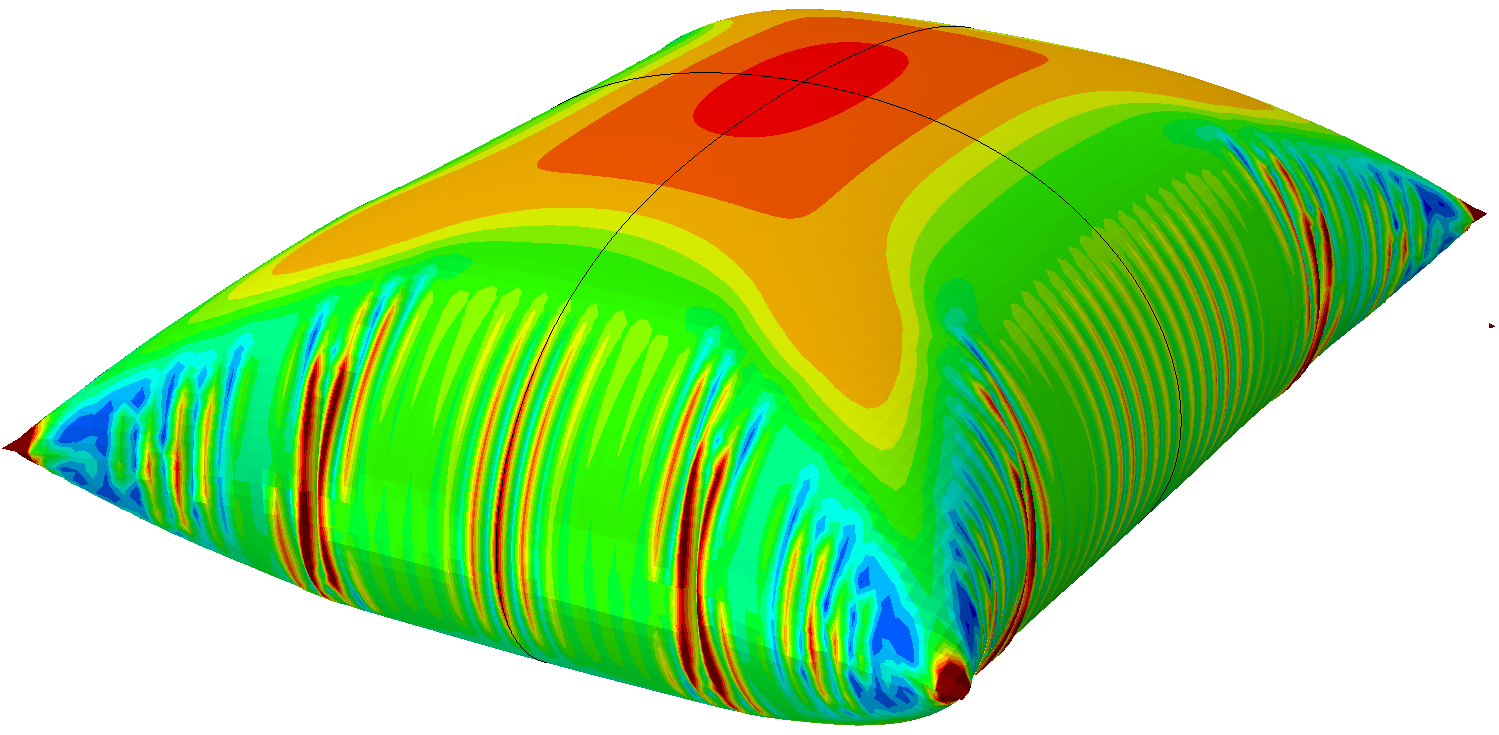
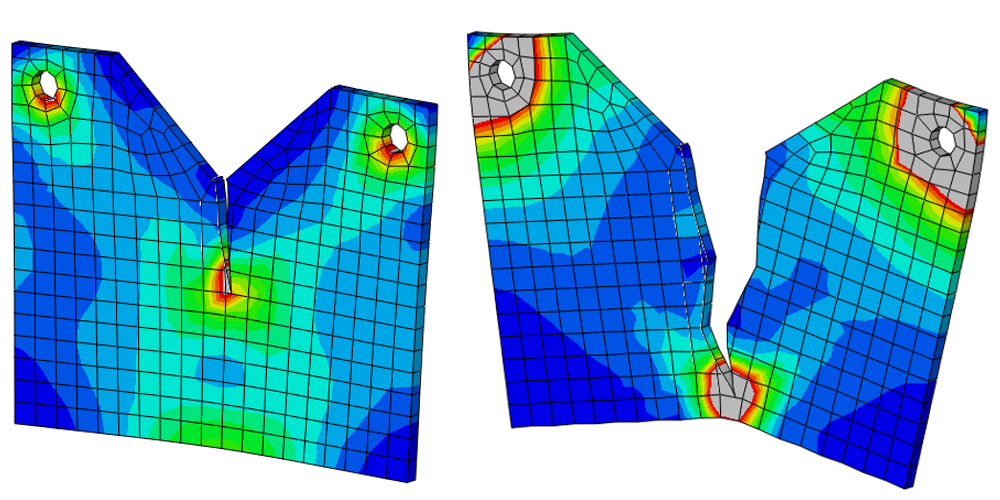
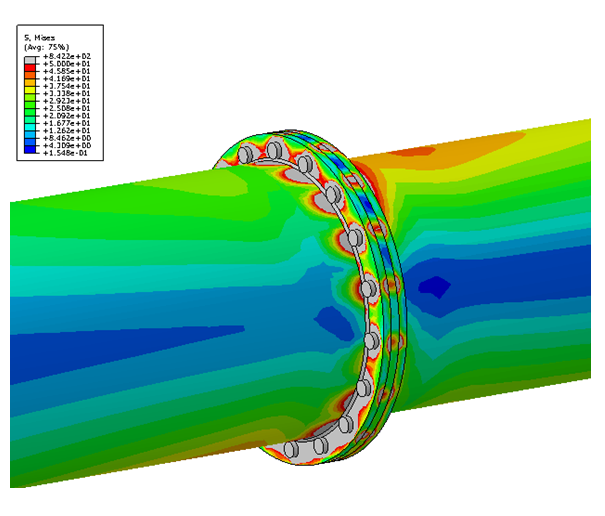
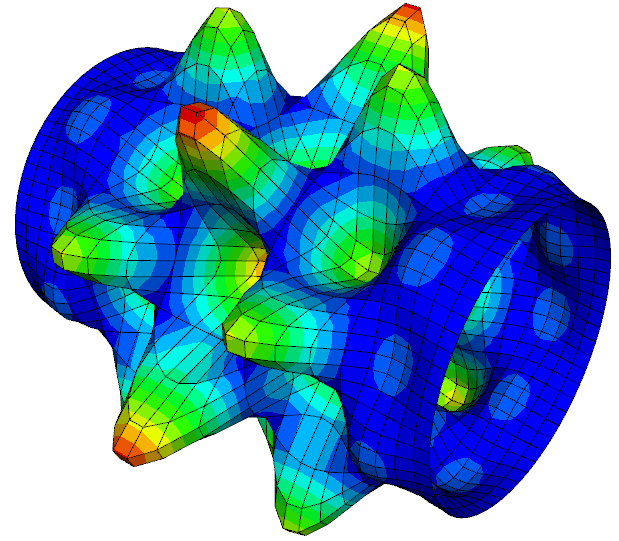
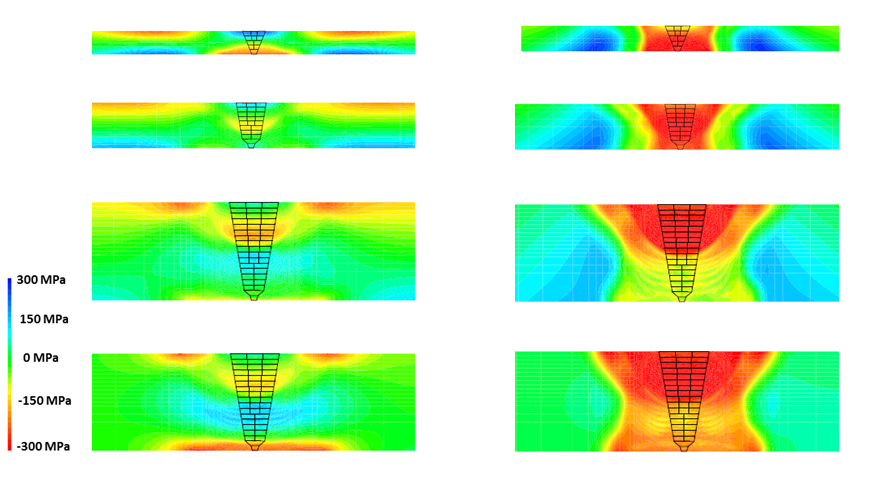
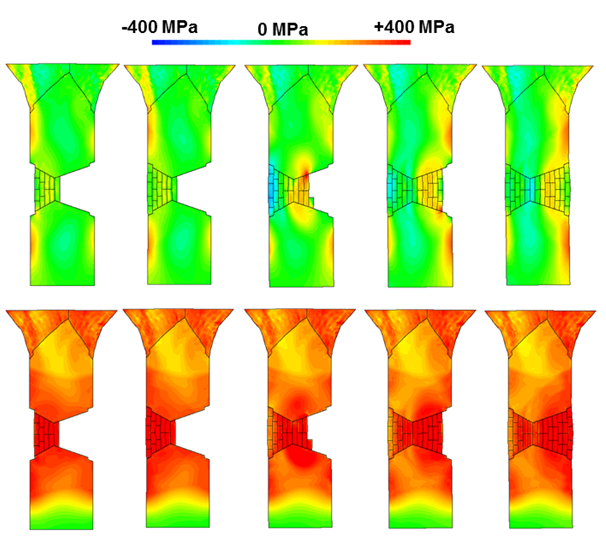
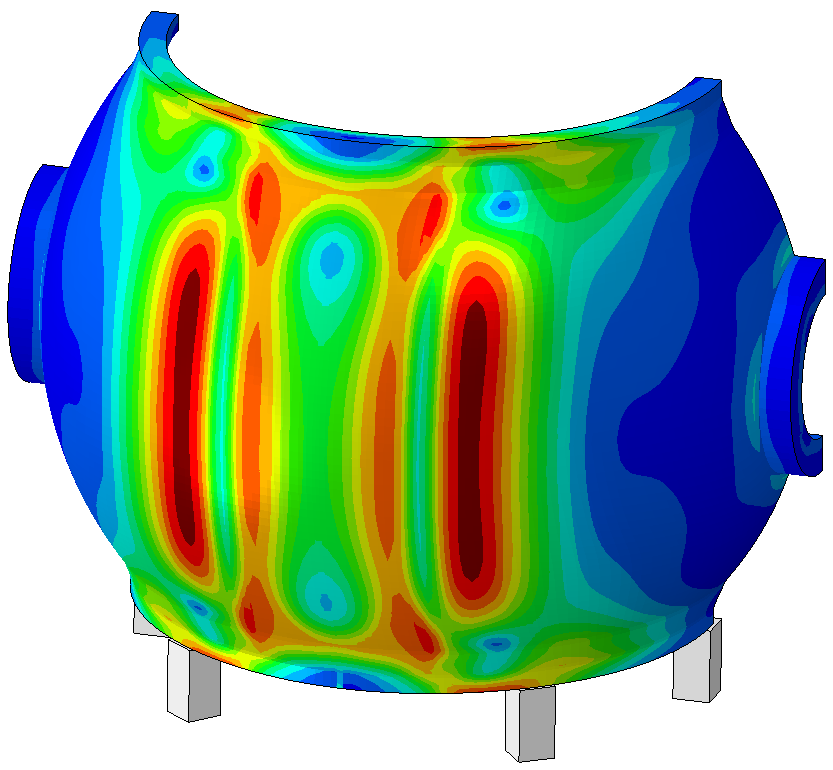
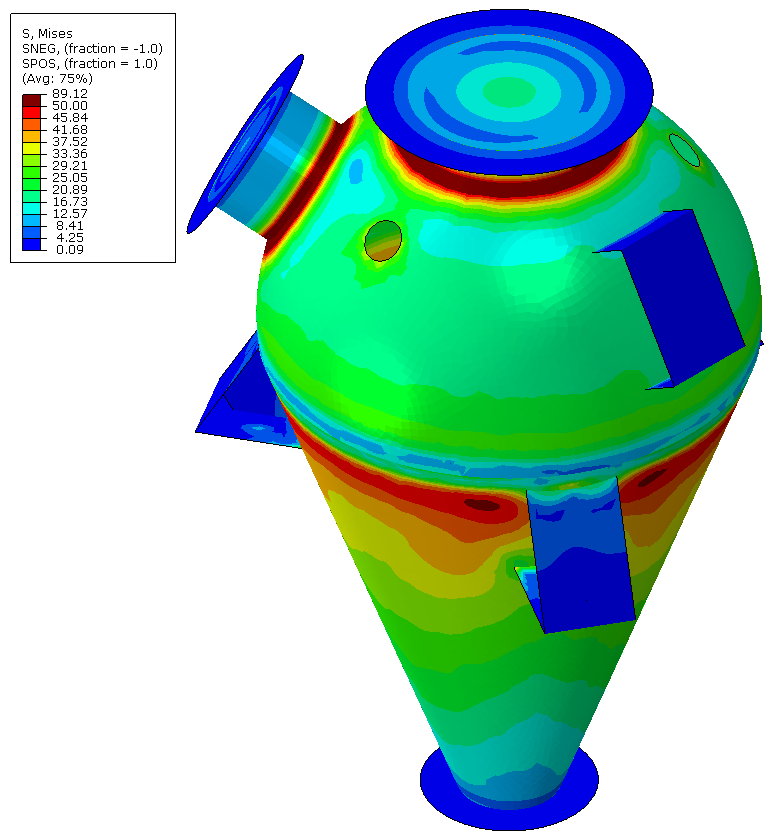
- sous forme de champs : déplacements(mm), contraintes de Von Mises (MPa), contraintes maximales principales (traction, MPa) et minimales principales (compression, MPa), pressions de contact (MPa), déformation élastiques (%), déformations plastiques cumulées (%), etc.
- sous forme de graphiques : énergies (interne, plastique, de fortement, cinétique, totale, ...), positions, vitesses, accélérations, efforts résultants, etc.
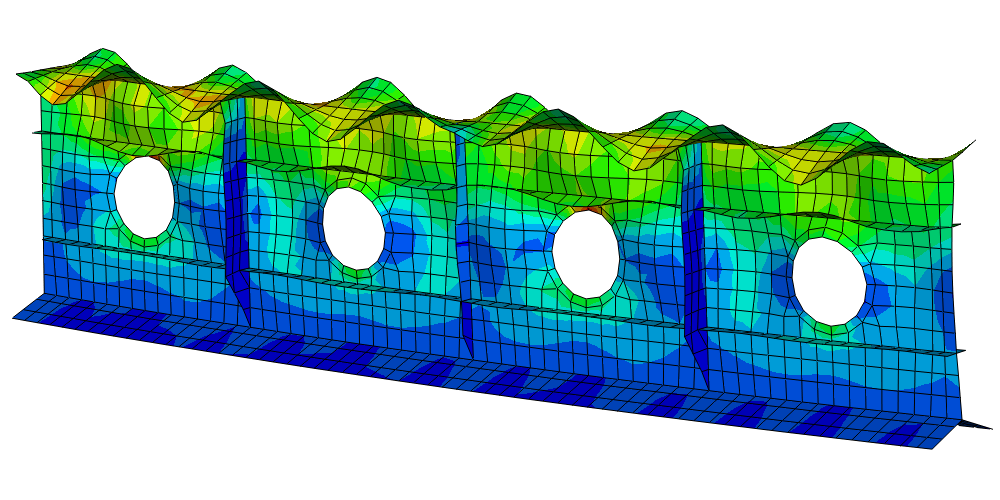
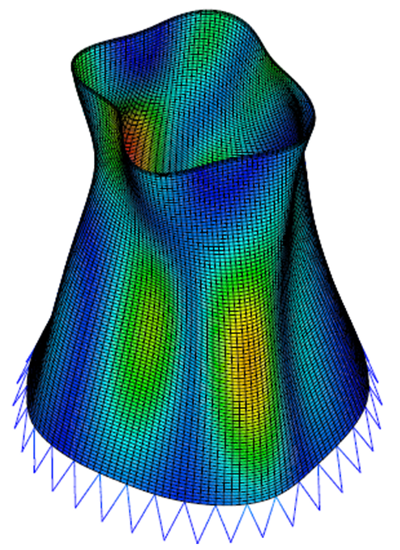
En fonction du phénomène étudié, différents critères de tenue sont définis : par exemple, pour un calcul statique (poutre en flexion etc…), les champs de déformations de la structure et les contraintes sont généralement étudiés pour valider ou non la tenue mécanique de la structure.
Il faut néanmoins être conscient que la méthode des éléments finis est une solution approchée d’un problème : il est nécessaire de vérifier la précision du calcul en validant la convergence du maillage et la cohérence des résultats (continuité des déformations dans la matière, ...).
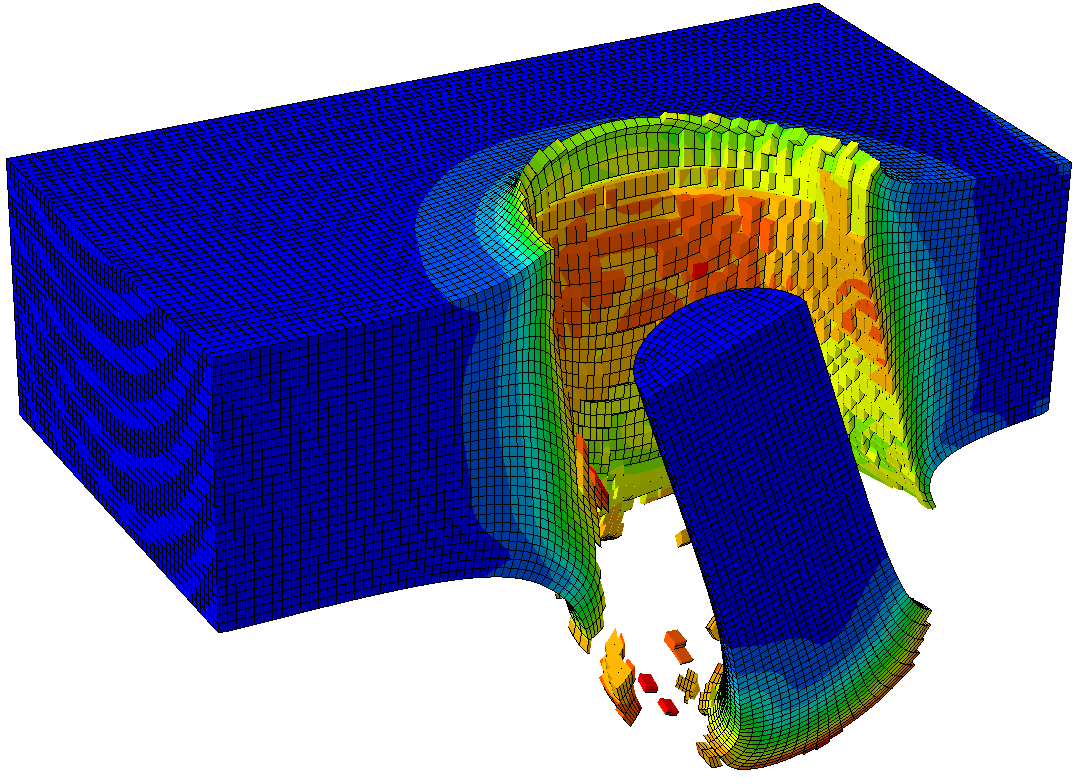
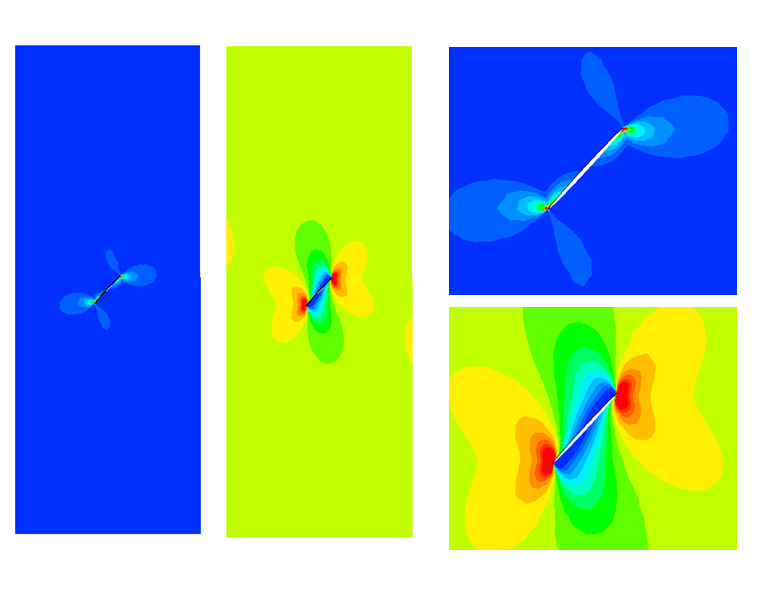
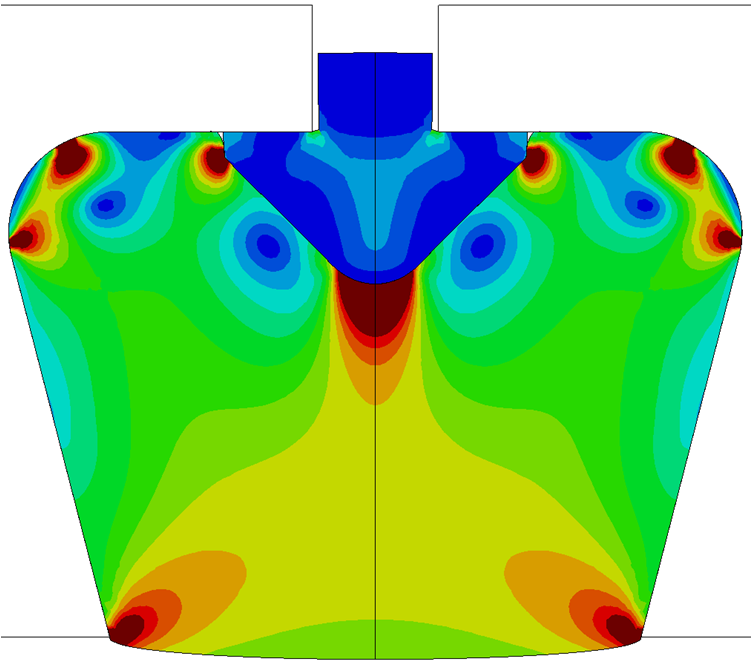
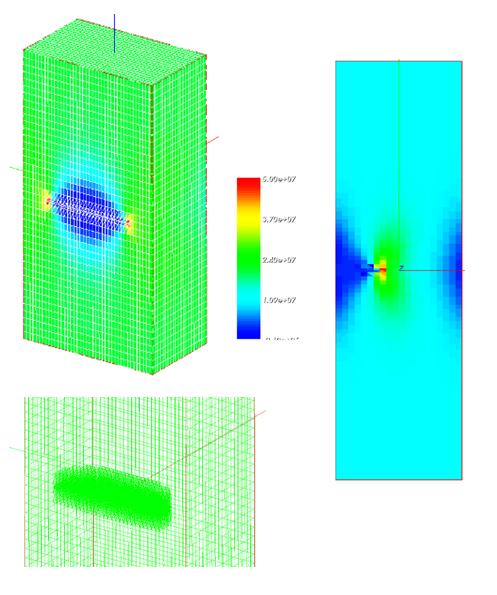
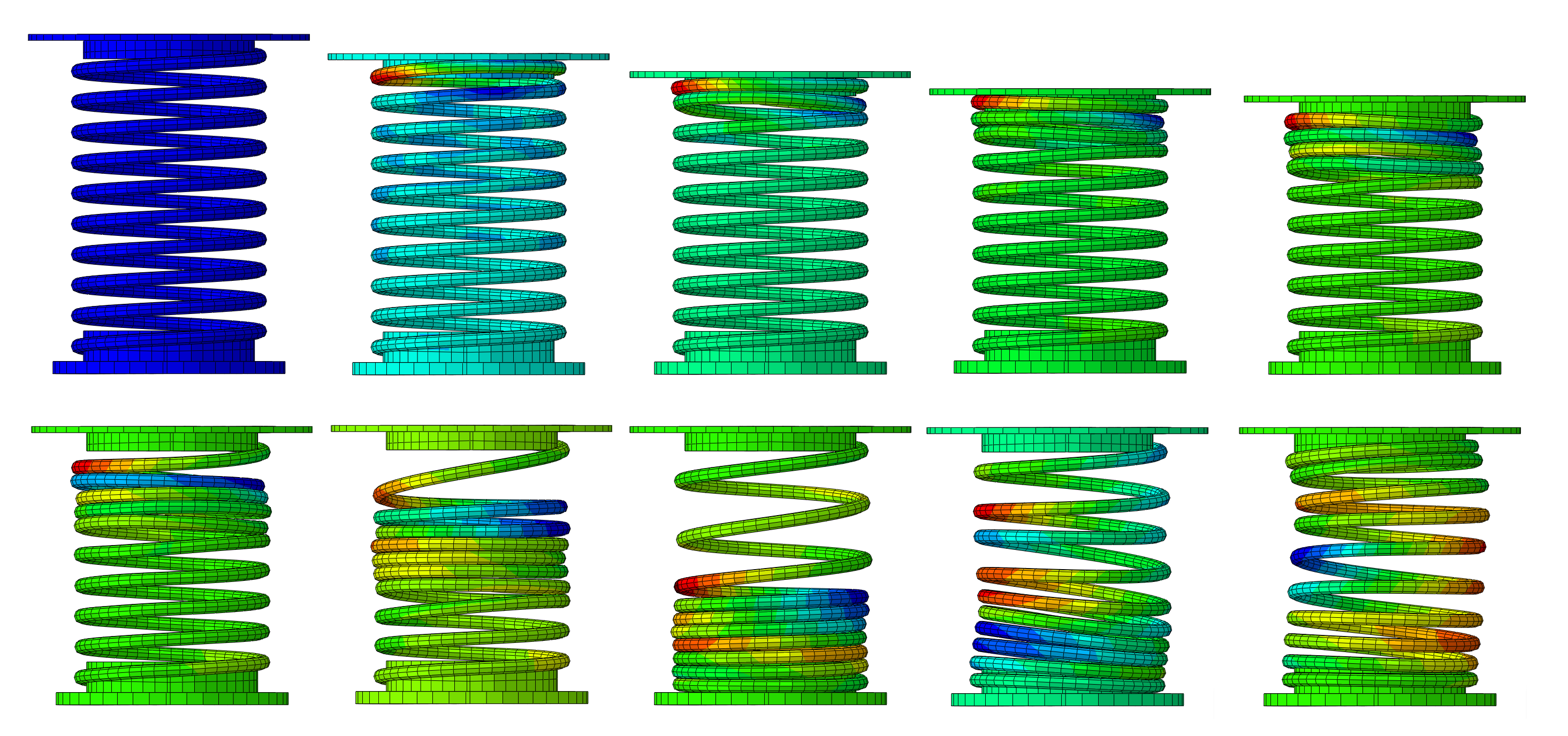
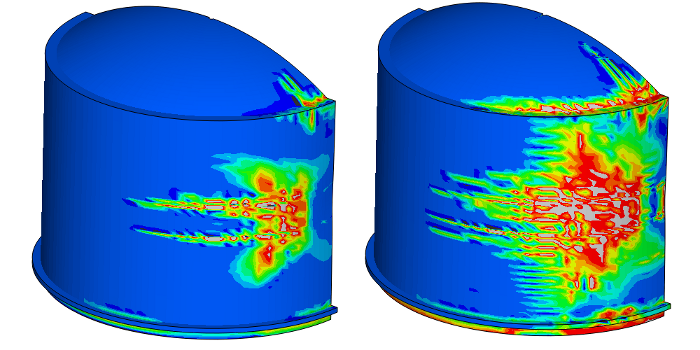
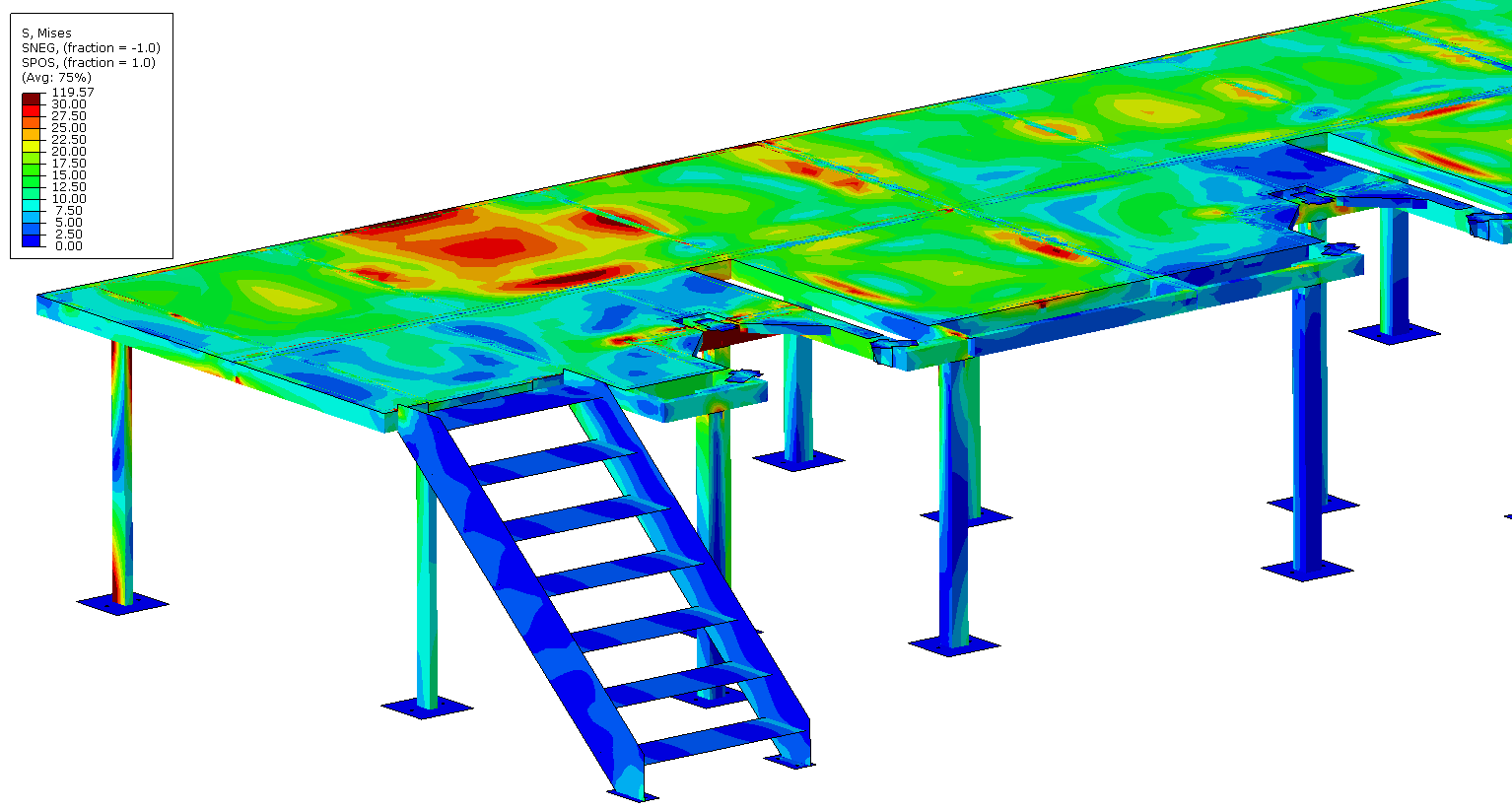
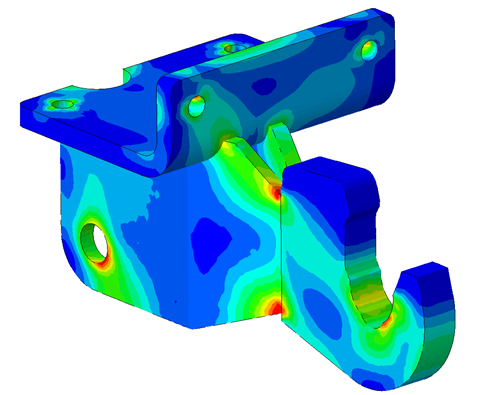
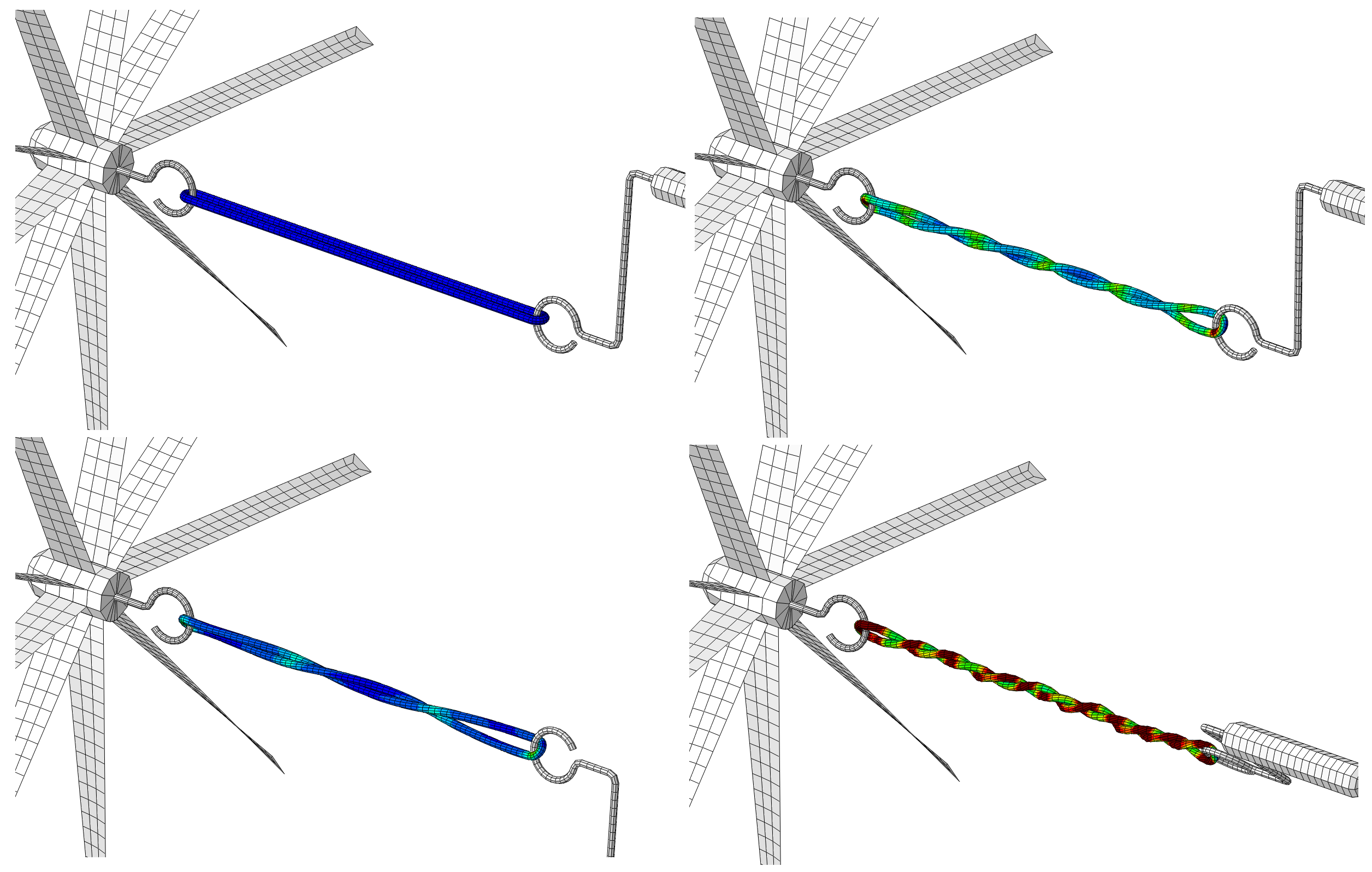
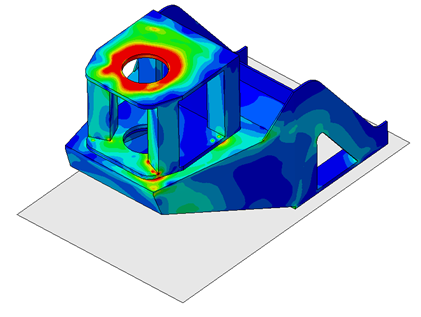
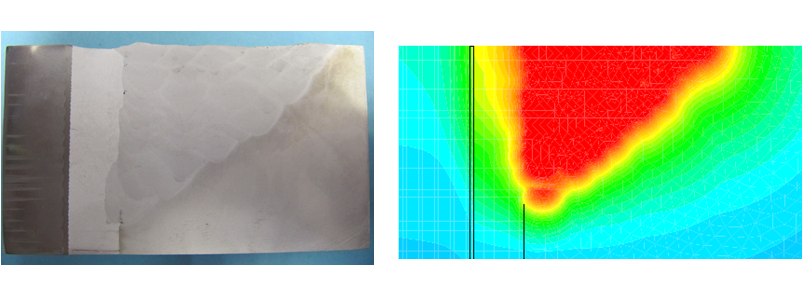
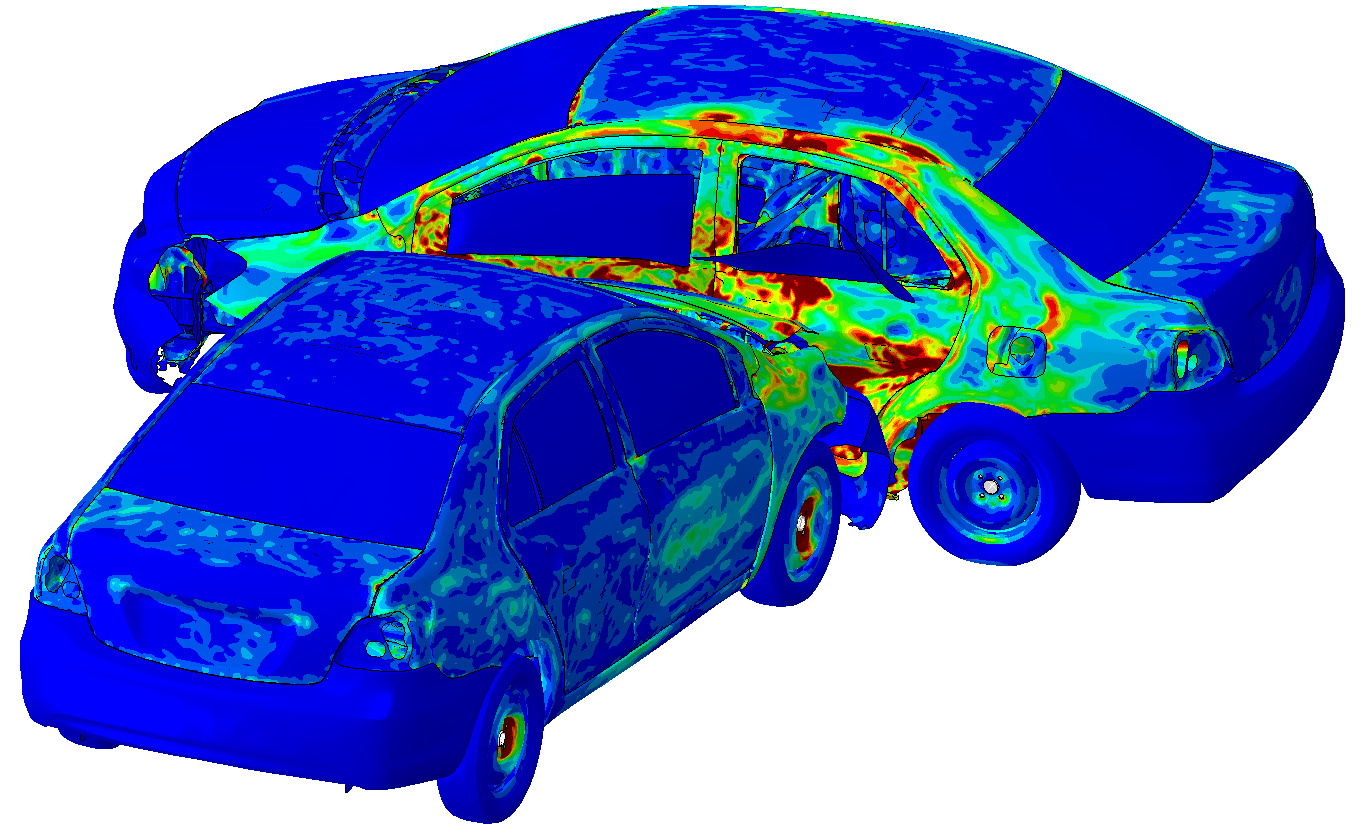
Ci-dessous, vous trouverez quelques exemples d'études et de cas tests menés par EC2 :